复杂度分析
为什么需要复杂度分析
有人说可以通过让代码跑一遍,然后进行统计和监控来得到结果。然后跑多次来进行结果的对比。这种方法叫做事后统计法。
这种方法有很严重的缺陷:
- 测试结果非常依赖于环境;
- 测试结果非常受数据规模的影响;
大O复杂度表示法
不运行代码的情况下,一眼能看出来代码的执行效率。
方法可以把代码运行的每一行代码的时间都认为是时间一样的,暂且当做unit_time。那么以下代码执行了多长时间呢:
1
2
3
4
5
6
7
8
int cal(int n) {
int sum = 0;
int i = 1;
for (; i <= n; ++i) {
sum = sum + i;
}
return sum;
}
最后的时间是(2n+2)*unit_time。
1
2
3
4
5
6
7
8
9
10
11
int cal(int n) {
int sum = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i) {
j = 1;
for (; j <= n; ++j) {
sum = sum + i * j;
}
}
}
以上的代码的执行时间为:T(n) = (2n2+2n+3)*unit_time。
而不管是(2n+2)unit_time还是(2n2+2n+3)unit_time。我们都可以把其描述为f(n)的一个函数。
即大O表示O(f(n));更具体的解释为:O(2n+2)和O(2n2+2n+3)。
通常只需要考虑增长最快的因素即可,常量、系数已经变化较小的公式都可以舍去,于是上面的大O表示法可以表示为:T(n) = O(n); T(n) = O(n2)
需要注意的是,这个大O表示法并不直接代表代码运行的时间,它只是代表随着数据规模的变化而代码执行消耗时间的趋势,叫做渐进时间复杂度也叫时间负责度。
快速判断时间复杂度的小技巧:
只关注运行代码随着数据规模增长最快的部分即可。
常见的时间复杂度案例分析

上面的复杂度可以分为两种:多项式量级和非多项式量级。
当数据规模 n 越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。
O(1)
O(1)并不是只执行了一行代码,只是常量级的时间复杂度表示方法。如下代码:
1
2
3
int i = 8;
int j = 6;
int sum = i + j;
只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)。或者说,一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
O(logn)、O(nlogn)
1
2
3
4
i=1;
while (i <= n) {
i = i * 2;
}
其实我们就是这个循环里面的代码执行了几次:x=log2n;
1
2
3
4
5
i=1;
while (i <= n) {
i = i * 3;
}
// 这段代码的时间复杂度为 O(log3n)。
不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复杂度都记为 O(logn)。
如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了;
O(m+n)、O(m*n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int cal(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}
m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n));
但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。
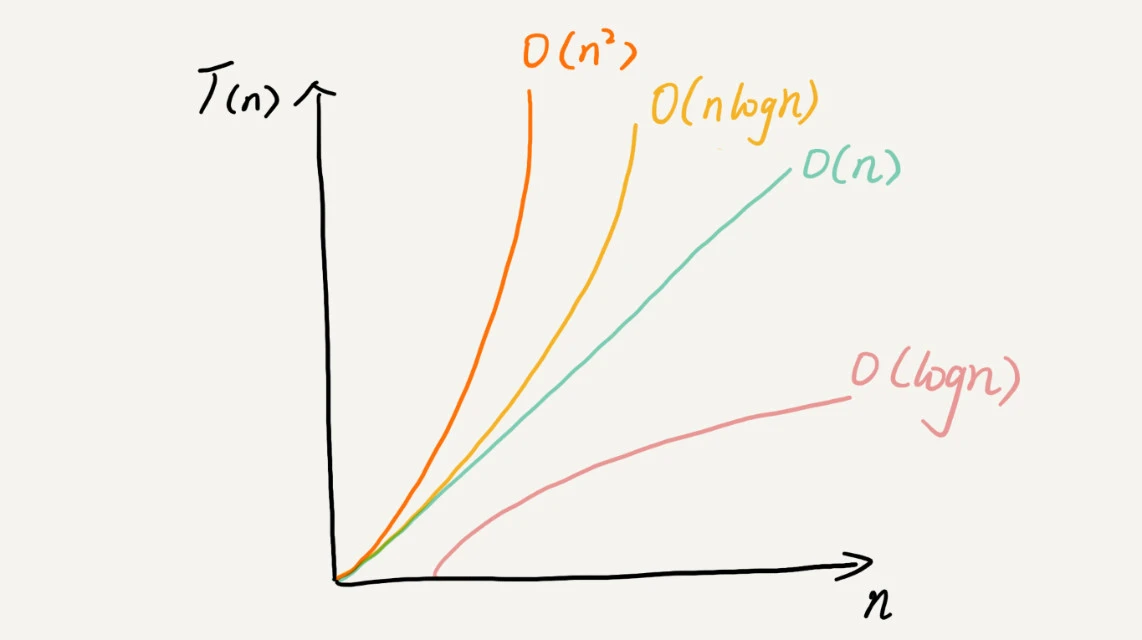
更详细的时间复杂度分析
- 最好情况时间复杂度
- 最坏情况时间复杂度
- 平均情况时间复杂度
- 均摊时间复杂度